| NCERT Exemplar Solutions | ||||||
|---|---|---|---|---|---|---|
| 6th | 7th | 8th | 9th | 10th | 11th | 12th |
| Content On This Page | ||
|---|---|---|
| Section A | Section B | Section C |
| Section D | ||
Class 10th Mathematics Sample Paper Set I (NCERT Exemplar)
Welcome to this critical section featuring a collection of Class 10 Mathematics Sample Papers, meticulously constructed to provide students with a truly realistic assessment experience. These papers are not merely practice sets; they are carefully designed to mirror the difficulty level, diverse question typology, and chapter-wise weightage anticipated in culminating examinations, especially those incorporating Higher-Order Thinking Skills (HOTS) and challenging application-based questions characteristic of the renowned NCERT Exemplar series. The objective is to move beyond rote learning and evaluate genuine conceptual understanding and problem-solving prowess across the entire syllabus, preparing students for the rigours of contemporary assessment patterns.
Accompanying each sample paper is an exhaustive set of comprehensive solutions. These solutions offer complete, step-by-step answers and detailed explanations for every single question within the respective paper. This support spans all possible question formats, ensuring thorough preparation:
- Multiple Choice Questions (MCQs)
- Fill-in-the-Blanks
- True/False Statements
- Very Short Answer Questions (VSA)
- Short Answer Questions (SA)
- Long Answer Questions (LA)
The solutions meticulously demonstrate the application of concepts, formulas, theorems, and strategic problem-solving approaches required to successfully tackle the varied questions presented. They serve as an invaluable guide to understanding how to approach different types of problems effectively.
These sample papers provide comprehensive coverage of the entire Class 10 Mathematics syllabus, drawing questions that reflect the depth and style of the NCERT Exemplar across all key domains. Expect to encounter challenges drawn from:
- Real Numbers (including Euclid's Lemma, Fundamental Theorem of Arithmetic)
- Polynomials (zeros, coefficients, division algorithm)
- Pairs of Linear Equations in Two Variables (consistency, solving methods)
- Quadratic Equations (roots, discriminant $D = b^2-4ac$, quadratic formula $x = \frac{-b \pm \sqrt{D}}{2a}$)
- Arithmetic Progressions ($a_n = a+(n-1)d$, $S_n = \frac{n}{2}[2a+(n-1)d]$)
- Triangles (Similarity criteria, BPT, Pythagoras Theorem $a^2+b^2=c^2$)
- Coordinate Geometry (Distance, Section, Area formulas)
- Introduction to Trigonometry & its Applications (Identities like $\sin^2\theta + \cos^2\theta = 1$, Heights and Distances)
- Circles (Tangents and their properties, e.g., tangents from an external point are equal)
- Constructions (using only ruler and compasses, justifications)
- Areas Related to Circles (sectors, segments, combination figures, Area = $\pi r^2$)
- Surface Areas & Volumes (combinations/conversions of solids, frustum, e.g., Volume of Cone = $\frac{1}{3}\pi r^2 h$)
- Statistics (Mean, Median, Mode for grouped data, ogives)
- Probability (Theoretical probability $P(E) = \frac{n(E)}{n(S)}$, complex experiments)
The solutions provided aim for exceptional clarity, mirroring the standards expected in board examinations that incorporate HOTS questions. They focus not merely on delivering the final answer but on elucidating the entire problem-solving process. This includes showcasing necessary formula applications, detailing the steps in algebraic manipulations, providing logical justifications for geometric proofs or construction steps, plotting graphs where required, and ensuring clear, unambiguous explanations. Emphasis is placed on demonstrating how concepts from different chapters might be integrated within a single, more complex problem, a hallmark of the Exemplar standard.
By diligently engaging with these solved sample papers, students can achieve several critical preparation goals. They can effectively assess their overall preparedness across the breadth of the syllabus, gain a clear understanding of examination patterns and potential marking schemes, practice essential time management skills under simulated conditions, accurately identify areas of weakness when confronted with a mix of problems, learn effective strategies for presenting answers clearly and logically, and become thoroughly familiar with the type and difficulty level of questions that demand higher-order thinking and cross-topical application. These solved papers are, therefore, positioned as crucial final-stage preparation tools for comprehensive readiness.
Section A
Question 1. After how many decimal places will the decimal expansion of the number $\frac{47}{2^{3}5^{2}}$ terminate?
(A) 5
(B) 2
(C) 3
(D) 1
Answer:
Given:
The number $\frac{47}{2^{3}5^{2}}$.
To Find:
The number of decimal places after which the decimal expansion of the given number will terminate.
Solution:
A rational number $\frac{p}{q}$, where $p$ and $q$ are coprime integers and $q \neq 0$, has a terminating decimal expansion if and only if the prime factorization of the denominator $q$ is of the form $2^m 5^n$, where $m$ and $n$ are non-negative integers.
The given number is $\frac{47}{2^{3}5^{2}}$.
The numerator is $p = 47$. Since $47$ is a prime number and the prime factors of the denominator are $2$ and $5$, $47$ and $2^3 5^2$ are coprime.
The denominator is $q = 2^{3}5^{2}$.
The prime factorization of the denominator is already in the form $2^m 5^n$, where $m = 3$ and $n = 2$.
For a number of the form $\frac{p}{2^m 5^n}$ (in simplest form), the decimal expansion terminates after $\max(m, n)$ decimal places.
In this case, $m = 3$ and $n = 2$.
We need to find the maximum of these exponents:
$\max(m, n) = \max(3, 2)$
$\max(3, 2) = 3$
Therefore, the decimal expansion of $\frac{47}{2^{3}5^{2}}$ will terminate after $3$ decimal places.
Conclusion:
The decimal expansion of the number $\frac{47}{2^{3}5^{2}}$ will terminate after $3$ decimal places.
The correct option is (C) 3.
Question 2. Euclid’s division lemma states that for two positive integers a and b, there exist unique integers q and r such that a = bq + r, where
(A) 0 ≤ r ≤ a
(B) 0 < r < b
(C) 0 ≤ r ≤ b
(D) 0 ≤ r < b
Answer:
Given:
Euclid’s division lemma states that for two positive integers $a$ and $b$, there exist unique integers $q$ and $r$ such that $a = bq + r$.
To Find:
The condition on the remainder $r$ in the statement of Euclid's division lemma.
Solution:
Euclid's division lemma (also known as the Euclidean Algorithm) is a fundamental theorem in number theory. It precisely defines the relationship between the dividend ($a$), the divisor ($b$), the quotient ($q$), and the remainder ($r$) when one positive integer is divided by another.
The statement of Euclid's division lemma is:
For any two positive integers $a$ and $b$, there exist unique integers $q$ (quotient) and $r$ (remainder) such that:
$a = bq + r$
The crucial condition on the remainder $r$ is that it must be non-negative and strictly less than the divisor $b$. This ensures the uniqueness of $q$ and $r$.
The condition is expressed as:
$0 \leq r < b$
This means the remainder $r$ can be zero (when $a$ is perfectly divisible by $b$) or any positive integer less than $b$.
Conclusion:
The condition on the remainder $r$ in Euclid’s division lemma is $0 \leq r < b$.
The correct option is (D) $0 \leq r < b$.
Question 3. The number of zeroes, the polynomial p (x) = (x – 2)2 + 4 can have, is
(A) 1
(B) 2
(C) 0
(D) 3
Answer:
Given:
The polynomial $p(x) = (x – 2)^2 + 4$.
To Find:
The number of zeroes of the polynomial $p(x)$.
Solution:
A zero of a polynomial $p(x)$ is a value of $x$ for which $p(x) = 0$. To find the zeroes, we set the polynomial equal to zero:
$p(x) = 0$
$(x - 2)^2 + 4 = 0$
Now, we need to solve this equation for $x$. Let's isolate the term $(x - 2)^2$:
$(x - 2)^2 = -4$
Consider the left-hand side of the equation, $(x - 2)^2$. This represents the square of a real number $(x - 2)$. The square of any real number is always greater than or equal to zero.
$(x - 2)^2 \geq 0$
The right-hand side of the equation is $-4$, which is a negative number.
Since the square of a real number cannot be negative, there is no real value of $x$ for which $(x - 2)^2 = -4$.
Therefore, the equation $(x - 2)^2 + 4 = 0$ has no real solutions.
The zeroes of a polynomial are the values of $x$ for which $p(x) = 0$. Since there are no real values of $x$ that satisfy $p(x) = 0$, the polynomial has no real zeroes.
The number of real zeroes is $0$.
Conclusion:
The polynomial $p(x) = (x – 2)^2 + 4$ has $0$ real zeroes.
The correct option is (C) 0.
Question 4. A pair of linear equations a1x + b1y + c1 = 0; a2x + b2y + c2 = 0 is said to be inconsistent, if
(A) $\frac{a_{1}}{a_{2}} \neq \frac{b_{1}}{b_{2}}$
(B) $\frac{a_{1}}{a_{2}} \neq \frac{b_{1}}{b_{2}} = \frac{c_{1}}{c_{2}}$
(C) $\frac{a_{1}}{a_{2}} = \frac{b_{1}}{b_{2}} \neq \frac{c_{1}}{c_{2}}$
(D) $\frac{a_{1}}{a_{2}} \neq \frac{c_{1}}{c_{2}} $
Answer:
Given:
A pair of linear equations:
$a_1x + b_1y + c_1 = 0$
... (1)
$a_2x + b_2y + c_2 = 0$
... (2)
To Find:
The condition for the pair of linear equations to be inconsistent.
Solution:
A system of linear equations is said to be inconsistent if it has no solution. Graphically, this corresponds to two parallel lines that do not intersect.
For a pair of linear equations $a_1x + b_1y + c_1 = 0$ and $a_2x + b_2y + c_2 = 0$, the consistency and the nature of solutions are determined by comparing the ratios of the coefficients:
1. Unique Solution (Consistent): If the lines intersect at exactly one point, there is a unique solution. The condition for this is:
$\frac{a_{1}}{a_{2}} \neq \frac{b_{1}}{b_{2}}$
2. Infinitely Many Solutions (Consistent): If the lines are coincident (one lies exactly on top of the other), there are infinitely many solutions. The condition for this is:
$\frac{a_{1}}{a_{2}} = \frac{b_{1}}{b_{2}} = \frac{c_{1}}{c_{2}}$
3. No Solution (Inconsistent): If the lines are parallel and distinct (they never intersect), there is no solution. The condition for this is:
$\frac{a_{1}}{a_{2}} = \frac{b_{1}}{b_{2}} \neq \frac{c_{1}}{c_{2}}$
The question asks for the condition when the system is inconsistent, which means there is no solution.
Comparing the condition for no solution with the given options, we find that option (C) matches the condition for an inconsistent system.
$\frac{a_{1}}{a_{2}} = \frac{b_{1}}{b_{2}} \neq \frac{c_{1}}{c_{2}}$
Conclusion:
A pair of linear equations $a_1x + b_1y + c_1 = 0$ and $a_2x + b_2y + c_2 = 0$ is inconsistent if $\frac{a_{1}}{a_{2}} = \frac{b_{1}}{b_{2}} \neq \frac{c_{1}}{c_{2}}$.
The correct option is (C) $\frac{a_{1}}{a_{2}} = \frac{b_{1}}{b_{2}} \neq \frac{c_{1}}{c_{2}}$.
Question 5. The smallest value of k for which the equation x2 + kx + 9 = 0 has real roots, is
(A) – 6
(B) 6
(C) 36
(D) –3
Answer:
Given:
The quadratic equation $x^2 + kx + 9 = 0$.
To Find:
The smallest value of $k$ for which the equation has real roots.
Solution:
A quadratic equation of the form $ax^2 + bx + c = 0$ has real roots if and only if its discriminant, $\Delta$, is greater than or equal to zero.
The discriminant is given by the formula:
$\Delta = b^2 - 4ac$
For the given equation $x^2 + kx + 9 = 0$, we have:
$a = 1$
$b = k$
$c = 9$
For real roots, the discriminant must satisfy:
$\Delta \geq 0$
Substitute the values of $a$, $b$, and $c$ into the discriminant inequality:
$k^2 - 4(1)(9) \geq 0$
$k^2 - 36 \geq 0$
To solve this inequality, we can factor the left side:
$(k - 6)(k + 6) \geq 0$
The critical points are where the expression equals zero, which are $k - 6 = 0 \implies k = 6$ and $k + 6 = 0 \implies k = -6$.
We can analyze the sign of $(k - 6)(k + 6)$ in the intervals determined by the critical points $(-\infty, -6]$, $[-6, 6]$, and $[6, \infty)$.
| Interval | Sign of $(k-6)$ | Sign of $(k+6)$ | Sign of $(k-6)(k+6)$ | Condition $\geq 0$ |
| $k < -6$ | $-$ | $-$ | $+$ | True |
| $-6 \leq k \leq 6$ | $-$ | $+$ | $-$ | False (for $<0$) |
| $k > 6$ | $+$ | $+$ | $+$ | True |
The inequality $k^2 - 36 \geq 0$ is satisfied when $k \leq -6$ or $k \geq 6$.
So, the values of $k$ for which the equation has real roots are $k \in (-\infty, -6] \cup [6, \infty)$.
We are looking for the smallest value of $k$ among the options for which the equation has real roots. The possible values of $k$ are any number less than or equal to $-6$ or any number greater than or equal to $6$.
Comparing this with the options:
(A) $-6$: This value is in the set of valid $k$ values ($k \leq -6$). It is the largest value in the interval $(-\infty, -6]$.
(B) $6$: This value is in the set of valid $k$ values ($k \geq 6$). It is the smallest value in the interval $[6, \infty)$.
(C) $36$: This value is in the set of valid $k$ values ($k \geq 6$).
(D) $-3$: This value is not in the set of valid $k$ values ($-6 < -3 < 6$).
The question asks for the "smallest value of k". Considering the union of the intervals, the values range from $-\infty$ up to $-6$ and from $6$ up to $\infty$. Among the options provided that satisfy the condition, $-6$ is the smallest value.
Note: If the question was phrased differently, e.g., asking for the minimum absolute value of $k$ or the smallest non-negative value of $k$, the answer might be $6$. But "smallest value" generally refers to the value lowest on the number line.
The possible values for $k$ are all numbers in $(-\infty, -6]$ and $[6, \infty)$. The options are $-6$, $6$, $36$, $-3$. We check which of these satisfy $k \leq -6$ or $k \geq 6$.
- For $k = -6$: $-6 \leq -6$ is true. So, $k = -6$ gives real roots.
- For $k = 6$: $6 \geq 6$ is true. So, $k = 6$ gives real roots.
- For $k = 36$: $36 \geq 6$ is true. So, $k = 36$ gives real roots.
- For $k = -3$: $-3 \leq -6$ is false, and $-3 \geq 6$ is false. So, $k = -3$ does not give real roots.
The values from the options that result in real roots are $-6$, $6$, and $36$. Among these values, the smallest is $-6$.
Conclusion:
The smallest value of $k$ for which the equation $x^2 + kx + 9 = 0$ has real roots is $-6$.
The correct option is (A) – 6.
Question 6. The coordinates of the points P and Q are (4, –3) and (–1, 7). Then the abscissa of a point R on the line segment PQ such that $\frac{PR}{PQ}$ = $\frac{3}{5}$ is
(A) $\frac{18}{5}$
(B) $\frac{17}{5}$
(C) $\frac{17}{8}$
(D) 1
Answer:
Given:
Coordinates of point P are $(4, -3)$. Let $P = (x_1, y_1) = (4, -3)$.
Coordinates of point Q are $(-1, 7)$. Let $Q = (x_2, y_2) = (-1, 7)$.
A point R is on the line segment PQ such that $\frac{PR}{PQ} = \frac{3}{5}$.
To Find:
The abscissa (x-coordinate) of point R.
Solution:
We are given that the point R lies on the line segment PQ and the ratio $\frac{PR}{PQ} = \frac{3}{5}$.
This means that the length of segment PR is 3 parts, and the length of the entire segment PQ is 5 parts.
Since R is on the segment PQ, the length of segment RQ must be the total length minus the length of PR.
$RQ = PQ - PR$
In terms of parts, $RQ = 5 \text{ parts} - 3 \text{ parts} = 2 \text{ parts}$.
So, the ratio of the lengths of the segments PR and RQ is:
$\frac{PR}{RQ} = \frac{3 \text{ parts}}{2 \text{ parts}} = \frac{3}{2}$
This indicates that the point R divides the line segment PQ internally in the ratio $3 : 2$.
Let $m_1 = 3$ and $m_2 = 2$.
We use the section formula for internal division. If a point $R(x, y)$ divides the line segment joining $P(x_1, y_1)$ and $Q(x_2, y_2)$ internally in the ratio $m_1 : m_2$, the coordinates of R are given by:
$x = \frac{m_1x_2 + m_2x_1}{m_1 + m_2}$
... (Section Formula for x)
$y = \frac{m_1y_2 + m_2y_1}{m_1 + m_2}$
... (Section Formula for y)
We only need the abscissa (x-coordinate) of R. Substitute the given values into the formula for $x$:
$x = \frac{(3)(-1) + (2)(4)}{3 + 2}$
$x = \frac{-3 + 8}{5}$
$x = \frac{5}{5}$
$x = 1$
The abscissa of the point R is 1.
Conclusion:
The abscissa of the point R on the line segment PQ such that $\frac{PR}{PQ} = \frac{3}{5}$ is 1.
The correct option is (D) 1.
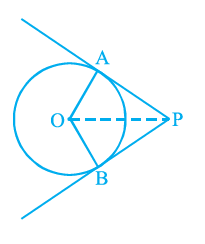
Question 7. In the adjoining figure, PA and PB are tangents from a point P to a circle with centre O. Then the quadrilateral OAPB must be a
(A) square
(B) rhombus
(C) cyclic quadrilateral
(D) parallelogram
Answer:
Given:
PA and PB are tangents drawn from an external point P to a circle with centre O. OAPB is a quadrilateral formed by joining the points O, A, P, and B.
To Determine:
The type of quadrilateral OAPB.
Solution:
We know the following properties related to tangents drawn from an external point to a circle:
1. The radius through the point of contact is perpendicular to the tangent.
Therefore, the radius OA is perpendicular to the tangent PA, and the radius OB is perpendicular to the tangent PB.
$\angle OAP = 90^\circ$
$\angle OBP = 90^\circ$
Now consider the quadrilateral OAPB. The sum of the interior angles of any quadrilateral is $360^\circ$.
So, in quadrilateral OAPB:
$\angle AOB + \angle OAP + \angle APB + \angle OBP = 360^\circ$
Substitute the values of $\angle OAP$ and $\angle OBP$:
$\angle AOB + 90^\circ + \angle APB + 90^\circ = 360^\circ$
$\angle AOB + \angle APB + 180^\circ = 360^\circ$
$\angle AOB + \angle APB = 360^\circ - 180^\circ$
$\angle AOB + \angle APB = 180^\circ$
We have found that the sum of the opposite angles $\angle AOB$ and $\angle APB$ is $180^\circ$.
We also know that the sum of the other pair of opposite angles is $\angle OAP + \angle OBP = 90^\circ + 90^\circ = 180^\circ$.
A quadrilateral is called a cyclic quadrilateral if the sum of each pair of opposite angles is $180^\circ$.
Since both pairs of opposite angles ($\angle OAP$ and $\angle OBP$; $\angle AOB$ and $\angle APB$) sum up to $180^\circ$, the quadrilateral OAPB is a cyclic quadrilateral.
Let's consider the other options:
- Square: A square requires all angles to be $90^\circ$ and all sides equal (OA=AP=PB=BO). While $\angle OAP = \angle OBP = 90^\circ$, $\angle AOB$ and $\angle APB$ are not necessarily $90^\circ$. Also, OA (radius) is not necessarily equal to AP (tangent length).
- Rhombus: A rhombus requires all sides to be equal (OA=AP=PB=BO). Again, OA is not necessarily equal to AP.
- Parallelogram: A parallelogram requires opposite angles to be equal and opposite sides parallel. While $\angle OAP = \angle OBP = 90^\circ$ (so opposite angles are equal), $\angle AOB$ is not necessarily equal to $\angle APB$.
The property that the sum of opposite angles is $180^\circ$ always holds for OAPB when PA and PB are tangents from P. This confirms that OAPB is a cyclic quadrilateral.
Conclusion:
The quadrilateral OAPB must be a cyclic quadrilateral.
The correct option is (C) cyclic quadrilateral.
Question 8. If for some angle θ , cot 2θ = $\frac{1}{\sqrt{3}}$ then the value of sin 3θ ,where 2θ ≤ 90° is
(A) $\frac{1}{\sqrt{2}}$
(B) 1
(C) 0
(D) $\frac{\sqrt{3}}{2}$
Answer:
Given:
$\cot 2\theta = \frac{1}{\sqrt{3}}$ and $2\theta \leq 90^\circ$.
To Find:
The value of $\sin 3\theta$.
Solution:
We are given that $\cot 2\theta = \frac{1}{\sqrt{3}}$.
We know the standard trigonometric values for common angles. The cotangent of $60^\circ$ is $\frac{1}{\sqrt{3}}$.
$\cot 60^\circ = \frac{1}{\sqrt{3}}$
Comparing the given equation with the standard value, we have:
$\cot 2\theta = \cot 60^\circ$
Since the angle $2\theta$ is in the range $2\theta \leq 90^\circ$, and the cotangent value is positive, $2\theta$ must be an angle in the first quadrant.
In the first quadrant, if $\cot A = \cot B$, then $A = B$.
Therefore, we can equate the angles:
$2\theta = 60^\circ$
Now, we can find the value of $\theta$:
$\theta = \frac{60^\circ}{2}$
$\theta = 30^\circ$
We need to find the value of $\sin 3\theta$. Substitute the value of $\theta$ we found:
$\sin 3\theta = \sin (3 \times 30^\circ)$
$\sin 3\theta = \sin 90^\circ$
We know the value of $\sin 90^\circ$:
$\sin 90^\circ = 1$
So, the value of $\sin 3\theta$ is 1.
Conclusion:
The value of $\sin 3\theta$ is 1.
The correct option is (B) 1.
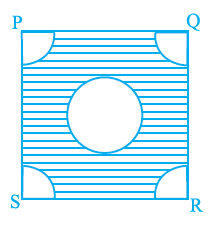
Question 9. From each corner of a square of side 4 cm, a quadrant of a circle of radius 1 cm is cut and also a circle of diameter 2 cm is cut as shown in figure. The area of the remaining (shaded) portion is
(A) (16 – 2π) cm2
(B) (16 – 5π) cm2
(C) 2π cm2
(D) 5π cm2
Answer:
Given:
A square of side 4 cm.
Four quadrants of a circle, each of radius 1 cm, are cut from the corners.
A circle of diameter 2 cm is cut from the center.
To Find:
The area of the remaining (shaded) portion of the square.
Solution:
Let the side of the square be $s$.
$s = 4$ cm
The area of the square is given by $s^2$.
Area of square = $(4 \text{ cm})^2 = 16 \text{ cm}^2$
From each corner, a quadrant of a circle of radius $r_q = 1$ cm is cut.
The area of one quadrant is $\frac{1}{4}$ of the area of a circle with radius $r_q$.
Area of one quadrant = $\frac{1}{4} \pi r_q^2 = \frac{1}{4} \pi (1)^2 = \frac{\pi}{4} \text{ cm}^2$
Since there are four such quadrants, the total area of the four quadrants is $4 \times (\text{Area of one quadrant})$. Note that four quadrants form a complete circle of radius 1 cm.
Total area of four quadrants = $4 \times \frac{\pi}{4} = \pi \text{ cm}^2$
From the center, a circle of diameter $d_c = 2$ cm is cut. The radius of this circle is $r_c = \frac{d_c}{2}$.
$r_c = \frac{2 \text{ cm}}{2} = 1 \text{ cm}$
The area of the circle cut from the center is $\pi r_c^2$.
Area of central circle = $\pi (1)^2 = \pi \text{ cm}^2$
The area of the remaining (shaded) portion is the area of the square minus the total area of the four quadrants minus the area of the central circle.
Area of remaining portion = Area of square - (Total area of 4 quadrants) - (Area of central circle)
Area of remaining portion = $16 \text{ cm}^2 - \pi \text{ cm}^2 - \pi \text{ cm}^2$
Area of remaining portion = $(16 - 2\pi) \text{ cm}^2$
Conclusion:
The area of the remaining (shaded) portion is $(16 - 2\pi) \text{ cm}^2$.
The correct option is (A) $(16 – 2\pi) \text{ cm}^2$.
Question 10. A letter of English alphabets is chosen at random. The probability that it is a letter of the word ‘MATHEMATICS’ is
(A) $\frac{11}{26}$
(B) $\frac{5}{13}$
(C) $\frac{9}{26}$
(D) $\frac{4}{13}$
Answer:
Given:
A letter is chosen at random from the English alphabets.
The word is 'MATHEMATICS'.
To Find:
The probability that the chosen letter is a letter of the word 'MATHEMATICS'.
Solution:
The total number of possible outcomes is the total number of letters in the English alphabet.
Total number of letters in English alphabet = 26
The favorable outcomes are the unique letters present in the word 'MATHEMATICS'.
Let's list the letters in the word 'MATHEMATICS': M, A, T, H, E, M, A, T, I, C, S.
Now, let's identify the unique letters:
M, A, T, H, E, I, C, S
Counting the number of unique letters, we have:
- M
- A
- T
- H
- E
- I
- C
- S
There are 8 unique letters in the word 'MATHEMATICS'.
Number of favorable outcomes = 8
The probability of an event is given by the formula:
Probability = $\frac{\text{Number of favorable outcomes}}{\text{Total number of possible outcomes}}$
Substitute the values we found:
Probability = $\frac{8}{26}$
Now, we simplify the fraction by dividing both the numerator and the denominator by their greatest common divisor, which is 2.
Probability = $\frac{\cancel{8}^4}{\cancel{26}_{13}}$
Probability = $\frac{4}{13}$
Conclusion:
The probability that a letter chosen at random from the English alphabets is a letter of the word 'MATHEMATICS' is $\frac{4}{13}$.
The correct option is (D) $\frac{4}{13}$.
Section B
Question 11. Is there any natural number n for which 4n ends with the digit 0? Give reasons in support of your answer.
Answer:
Given:
The expression $4^n$, where $n$ is a natural number ($n \in \{1, 2, 3, \dots\}$).
To Determine:
Whether there exists any natural number $n$ such that $4^n$ ends with the digit 0.
Solution:
A positive integer ends with the digit 0 if and only if its prime factorization contains both $2$ and $5$ as factors.
This is because any number ending in 0 is a multiple of 10, and the prime factorization of 10 is $2 \times 5$. So, the number must be divisible by both 2 and 5.
Let's consider the number $4^n$. We need to find the prime factorization of $4^n$.
First, find the prime factors of the base, 4.
$4 = 2 \times 2 = 2^2$
Now, substitute this into the expression $4^n$:
$4^n = (2^2)^n$
Using the exponent rule $(a^m)^n = a^{mn}$, we get:
$4^n = 2^{2n}$
The prime factorization of $4^n$ is $2^{2n}$. This means that the only prime factor of $4^n$ is 2.
For $4^n$ to end with the digit 0, its prime factorization must contain both 2 and 5.
Since the prime factorization of $4^n$ is $2^{2n}$, it only contains the prime factor 2. It does not contain the prime factor 5.
According to the Unique Factorization Theorem (Fundamental Theorem of Arithmetic), the prime factorization of any composite number is unique.
Therefore, $4^n$ cannot have 5 as a prime factor.
Since 5 is not a prime factor of $4^n$, $4^n$ is not divisible by 5.
A number must be divisible by both 2 and 5 to end with the digit 0.
As $4^n$ is not divisible by 5, $4^n$ cannot end with the digit 0 for any natural number $n$.
For example:
- For $n=1$, $4^1 = 4$. Ends with 4.
- For $n=2$, $4^2 = 16$. Ends with 6.
- For $n=3$, $4^3 = 64$. Ends with 4.
- For $n=4$, $4^4 = 256$. Ends with 6.
The last digit will always be 4 or 6.
Conclusion:
No, there is no natural number $n$ for which $4^n$ ends with the digit 0.
The reason is that for a number to end with the digit 0, its prime factorization must include both 2 and 5. The prime factorization of $4^n$ is $2^{2n}$, which only contains the prime factor 2 and does not contain the prime factor 5.
Question 12. Without using the formula for the nth term, find which term of the AP : 5, 17, 29, 41, ... will be 120 more than its 15th term? Justify your answer.
OR
Is 144 a term of the AP : 3, 7, 11, ... ? Justify your answer.
Answer:
Given:
An arithmetic progression (AP): 5, 17, 29, 41, ...
To Find:
Which term of the given AP will be 120 more than its 15th term.
Solution:
Let the given AP be denoted by $a_1, a_2, a_3, \dots$.
The first term is $a_1 = 5$.
The common difference $d$ is the difference between consecutive terms:
$d = a_2 - a_1 = 17 - 5 = 12$
$d = a_3 - a_2 = 29 - 17 = 12$
So, the common difference $d = 12$.
Let the term that is 120 more than the 15th term be the $k$-th term, $a_k$.
According to the problem statement:
$a_k = a_{15} + 120$
Rearranging this equation, we get the difference between the $k$-th term and the 15th term:
$a_k - a_{15} = 120$
Justification (without using the formula for the nth term $a_n = a + (n-1)d$):
In an arithmetic progression, each term is obtained by adding the common difference to the previous term.
$a_2 = a_1 + d$
$a_3 = a_2 + d = (a_1 + d) + d = a_1 + 2d$
Continuing this pattern, the difference between any term $a_k$ and a preceding term $a_m$ ($k > m$) is the sum of $(k - m)$ common differences.
$a_k - a_m = (k - m)d$
Using this property for $m = 15$, the difference between the $k$-th term ($a_k$) and the 15th term ($a_{15}$) is $(k - 15)$ times the common difference $d$.
$a_k - a_{15} = (k - 15)d$
We are given that $a_k - a_{15} = 120$ and we found $d = 12$. Substitute these values into the equation:
$(k - 15) \times 12 = 120$
... (i)
Now, we solve equation (i) for $k$:
$k - 15 = \frac{120}{12}$
Simplify the fraction:
$k - 15 = \frac{\cancel{120}^{10}}{\cancel{12}_{1}}$
$k - 15 = 10$
Add 15 to both sides:
$k = 10 + 15$
$k = 25$
So, the 25th term of the AP will be 120 more than its 15th term.
Conclusion:
The 25th term of the AP : 5, 17, 29, 41, ... will be 120 more than its 15th term.
Question 13. The coordinates of the points P, Q and R are (3, 4), (3, –4) and (–3, 4), respectively. Is the area of ∆PQR 24 sq. units? Justify your answer.
Answer:
Given:
The coordinates of the vertices of $\triangle$PQR are P(3, 4), Q(3, –4), and R(–3, 4).
To Determine:
If the area of $\triangle$PQR is 24 sq. units and justify the answer.
Solution:
We are given the coordinates of the vertices: P(3, 4), Q(3, –4), and R(–3, 4).
Let's examine the coordinates of the points:
- Points P(3, 4) and Q(3, –4) have the same x-coordinate (3). This means the line segment PQ is a vertical line.
- Points P(3, 4) and R(–3, 4) have the same y-coordinate (4). This means the line segment PR is a horizontal line.
Since the line segment PQ is vertical and the line segment PR is horizontal, they are perpendicular to each other. The angle formed at the vertex P is a right angle.
$\angle QPR = 90^\circ$
(PQ is vertical, PR is horizontal)
Thus, $\triangle$PQR is a right-angled triangle with the right angle at P.
In a right-angled triangle, the area can be calculated using the formula $\frac{1}{2} \times \text{base} \times \text{height}$, where the base and height are the lengths of the two sides forming the right angle.
Here, we can take PR as the base and PQ as the height (or vice-versa).
Calculate the length of PR using the distance formula for a horizontal segment (difference in x-coordinates):
$PR = |x_R - x_P| = |-3 - 3| = |-6| = 6$ units
Calculate the length of PQ using the distance formula for a vertical segment (difference in y-coordinates):
$PQ = |y_Q - y_P| = |-4 - 4| = |-8| = 8$ units
Now, calculate the area of $\triangle$PQR:
Area of $\triangle$PQR = $\frac{1}{2} \times PR \times PQ$
Area of $\triangle$PQR = $\frac{1}{2} \times 6 \times 8$
Area of $\triangle$PQR = $\frac{1}{2} \times 48$
Area of $\triangle$PQR = 24 sq. units
The calculated area of $\triangle$PQR is 24 sq. units, which matches the value given in the question.
Justification:
The points P(3, 4) and Q(3, -4) lie on the vertical line $x=3$. The distance between them is $|4 - (-4)| = |8| = 8$.
The points P(3, 4) and R(-3, 4) lie on the horizontal line $y=4$. The distance between them is $|3 - (-3)| = |6| = 6$.
Since PQ is a vertical line segment and PR is a horizontal line segment, they are perpendicular at P, forming a right angle. Thus, $\triangle$PQR is a right-angled triangle with legs PQ and PR.
The area of a right-angled triangle is half the product of its legs. Area = $\frac{1}{2} \times PQ \times PR = \frac{1}{2} \times 8 \times 6 = 24$ sq. units.
Conclusion:
Yes, the area of $\triangle$PQR is 24 sq. units.
Question 14. The length of a line segment is 10 units. If one end is (2, –3) and the abscissa of the other end is 10, then its ordinate is either 3 or –9. Give justification for the two answers.
Answer:
Given:
Length of the line segment = 10 units.
Coordinates of one end point P = $(2, -3)$.
Abscissa (x-coordinate) of the other end point Q is 10. Let the ordinate (y-coordinate) of Q be $y$. So, Q = $(10, y)$.
To Justify:
That the ordinate of the other end is either 3 or –9.
Solution:
Let the coordinates of the two end points of the line segment be $P(x_1, y_1) = (2, -3)$ and $Q(x_2, y_2) = (10, y)$.
The distance between two points $(x_1, y_1)$ and $(x_2, y_2)$ is given by the distance formula:
$D = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2}$
... (Distance Formula)
We are given that the distance $D = 10$. Substitute the coordinates of P and Q and the given distance into the formula:
$10 = \sqrt{(10 - 2)^2 + (y - (-3))^2}$
Simplify the terms inside the square root:
$10 = \sqrt{(8)^2 + (y + 3)^2}$
$10 = \sqrt{64 + (y + 3)^2}$
To eliminate the square root, square both sides of the equation:
$10^2 = 64 + (y + 3)^2$
$100 = 64 + (y + 3)^2$
Rearrange the equation to solve for $(y + 3)^2$:
$(y + 3)^2 = 100 - 64$
$(y + 3)^2 = 36$
Now, take the square root of both sides. Remember that the square root of a positive number has both a positive and a negative value:
$y + 3 = \pm \sqrt{36}$
$y + 3 = \pm 6$
This leads to two possible cases for the value of $y+3$:
Case 1:
$y + 3 = 6$
Subtract 3 from both sides:
$y = 6 - 3$
$y = 3$
Case 2:
$y + 3 = -6$
Subtract 3 from both sides:
$y = -6 - 3$
$y = -9$
Thus, the possible values for the ordinate $y$ are 3 and -9.
Justification:
The distance formula relates the coordinates of two points and the distance between them. When one of the coordinates of a point is unknown, substituting the given information into the distance formula results in an equation where the unknown coordinate is part of a squared term (like $(y_2 - y_1)^2$ or $(x_2 - x_1)^2$).
In this specific problem, we obtained the equation $(y + 3)^2 = 36$. Taking the square root of both sides to solve for the unknown $y$ introduces the $\pm$ sign, as both a positive number $(6)$ and its negative counterpart $(-6)$ will result in the same value $(36)$ when squared. Specifically, $6^2 = 36$ and $(-6)^2 = 36$.
Therefore, we get two separate linear equations, $y + 3 = 6$ and $y + 3 = -6$, leading to two distinct values for $y$: 3 and -9. These two values correspond to two different points $(10, 3)$ and $(10, -9)$ that are both exactly 10 units away from the point $(2, -3)$ and have an abscissa of 10.
This confirms that the ordinate of the other end can indeed be either 3 or –9, and both are valid solutions to the distance equation.
Question 15. What is the maximum value of $\frac{3}{cosec\;\theta}$ ? Justify your answer.
Answer:
Given:
The expression $\frac{3}{\text{cosec}\;\theta}$.
To Find:
The maximum value of the expression $\frac{3}{\text{cosec}\;\theta}$.
Solution:
The given expression is $\frac{3}{\text{cosec}\;\theta}$.
We know the trigonometric identity that relates $\text{cosec}\;\theta$ and $\sin\theta$:
$\text{cosec}\;\theta = \frac{1}{\sin\theta}$
Provided that $\sin\theta \neq 0$, we can substitute this identity into the given expression:
$\frac{3}{\text{cosec}\;\theta} = \frac{3}{\frac{1}{\sin\theta}}$
Simplifying the complex fraction:
$\frac{3}{\text{cosec}\;\theta} = 3 \sin\theta$
Now, the problem reduces to finding the maximum value of the expression $3 \sin\theta$.
We know that for any real angle $\theta$, the sine function $\sin\theta$ has a range of values between -1 and 1, inclusive.
$-1 \leq \sin\theta \leq 1$
To find the range of $3 \sin\theta$, we multiply the inequality by 3:
$3 \times (-1) \leq 3 \sin\theta \leq 3 \times 1$
$-3 \leq 3 \sin\theta \leq 3$
The maximum value that $3 \sin\theta$ can take is the upper bound of this range, which is 3.
This maximum value is achieved when $\sin\theta = 1$, which occurs at angles like $\theta = 90^\circ$, $450^\circ$, etc.
Justification:
The given expression $\frac{3}{\text{cosec}\;\theta}$ is equivalent to $3 \sin\theta$. The value of the sine function, $\sin\theta$, varies between -1 and 1. Since the coefficient of $\sin\theta$ is a positive constant (3), multiplying the range of $\sin\theta$ by 3 scales the range linearly. The maximum value of $\sin\theta$ is 1, so the maximum value of $3 \sin\theta$ is $3 \times 1 = 3$. Conversely, the minimum value of $\sin\theta$ is -1, leading to a minimum value of $3 \times (-1) = -3$ for the expression. Therefore, the expression $3 \sin\theta$ can take any value in the interval [-3, 3], and its greatest possible value is 3.
Conclusion:
The maximum value of $\frac{3}{\text{cosec}\;\theta}$ is 3.
Section C
Question 16. Find the zeroes of the polynomial p (x) = 4$\sqrt{3}$ x2 - 2$\sqrt{3}$ - 2$\sqrt{3}$ and verify the relationship between the zeroes and the coefficients.
OR
On dividing the polynomial f (x) = x3 – 5x2 + 6x – 4 by a polynomial g(x), the quotient q(x) and remainder r(x) are x – 3, –3x + 5, respectively. Find the polynomial g(x).
Answer:
Given:
The polynomial $p(x) = 4\sqrt{3} x^2 - 2\sqrt{6} x - 2\sqrt{3}$.
To Find:
The zeroes of the polynomial and verify the relationship between the zeroes and its coefficients.
Solution:
To find the zeroes of the polynomial $p(x)$, we set $p(x) = 0$.
$4\sqrt{3} x^2 - 2\sqrt{6} x - 2\sqrt{3} = 0$
... (1)
This is a quadratic equation of the form $ax^2 + bx + c = 0$, where $a = 4\sqrt{3}$, $b = -2\sqrt{6}$, and $c = -2\sqrt{3}$.
We can divide the entire equation by $2\sqrt{3}$ to simplify it:
$\frac{4\sqrt{3} x^2}{2\sqrt{3}} - \frac{2\sqrt{6} x}{2\sqrt{3}} - \frac{2\sqrt{3}}{2\sqrt{3}} = 0$
$2x^2 - \sqrt{2} x - 1 = 0$
Now, we can use the quadratic formula $x = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a}$ to find the zeroes of this simplified equation. Here, $a=2$, $b=-\sqrt{2}$, $c=-1$.
Calculate the discriminant, $\Delta = b^2 - 4ac$:
$\Delta = (-\sqrt{2})^2 - 4(2)(-1)$
$\Delta = 2 + 8$
$\Delta = 10$
Now, apply the quadratic formula:
$x = \frac{-(-\sqrt{2}) \pm \sqrt{10}}{2(2)}$
$x = \frac{\sqrt{2} \pm \sqrt{10}}{4}$
The two zeroes are:
$\alpha = \frac{\sqrt{2} + \sqrt{10}}{4}$
$\beta = \frac{\sqrt{2} - \sqrt{10}}{4}$
Verification of the relationship between zeroes and coefficients:
The relationship between the zeroes ($\alpha$, $\beta$) and the coefficients ($a$, $b$, $c$) of a quadratic polynomial $ax^2 + bx + c$ is given by:
Sum of zeroes = $\alpha + \beta = -\frac{b}{a}$
Product of zeroes = $\alpha \times \beta = \frac{c}{a}$
Using the zeroes we found:
Sum of zeroes = $\alpha + \beta = \frac{\sqrt{2} + \sqrt{10}}{4} + \frac{\sqrt{2} - \sqrt{10}}{4}$
$= \frac{(\sqrt{2} + \sqrt{10}) + (\sqrt{2} - \sqrt{10})}{4} = \frac{\sqrt{2} + \sqrt{10} + \sqrt{2} - \sqrt{10}}{4} = \frac{2\sqrt{2}}{4}$
Sum of zeroes = $\frac{\sqrt{2}}{2}$
Using the coefficients of the original polynomial $a = 4\sqrt{3}$, $b = -2\sqrt{6}$, $c = -2\sqrt{3}$:
$-\frac{b}{a} = -\frac{-2\sqrt{6}}{4\sqrt{3}} = \frac{2\sqrt{6}}{4\sqrt{3}}$
$= \frac{\sqrt{6}}{2\sqrt{3}} = \frac{\sqrt{2 \times 3}}{2\sqrt{3}} = \frac{\sqrt{2} \times \sqrt{3}}{2 \times \sqrt{3}} = \frac{\sqrt{2}}{2}$
$-\frac{b}{a} = \frac{\sqrt{2}}{2}$
The sum of zeroes calculated from the roots matches $-\frac{b}{a}$.
Now, calculate the product of zeroes:
Product of zeroes = $\alpha \times \beta = \left(\frac{\sqrt{2} + \sqrt{10}}{4}\right) \times \left(\frac{\sqrt{2} - \sqrt{10}}{4}\right)$
$= \frac{(\sqrt{2} + \sqrt{10})(\sqrt{2} - \sqrt{10})}{4 \times 4} = \frac{(\sqrt{2})^2 - (\sqrt{10})^2}{16} = \frac{2 - 10}{16} = \frac{-8}{16}$
Product of zeroes = $-\frac{1}{2}$
Using the coefficients of the original polynomial $a = 4\sqrt{3}$ and $c = -2\sqrt{3}$:
$\frac{c}{a} = \frac{-2\sqrt{3}}{4\sqrt{3}}$
$= \frac{-2}{4} = -\frac{1}{2}$
$\frac{c}{a} = -\frac{1}{2}$
The product of zeroes calculated from the roots matches $\frac{c}{a}$.
Thus, the relationship between the zeroes and the coefficients is verified.
Conclusion:
The zeroes of the polynomial $p(x) = 4\sqrt{3} x^2 - 2\sqrt{6} x - 2\sqrt{3}$ are $\frac{\sqrt{2} + \sqrt{10}}{4}$ and $\frac{\sqrt{2} - \sqrt{10}}{4}$. The relationships between the zeroes and coefficients have been verified.
Question 17. Solve the equations 5x – y = 5 and 3x – y = 3 graphically.
Answer:
Given:
A system of two linear equations:
$5x - y = 5$
... (1)
$3x - y = 3$
... (2)
To Find:
The solution to the system of equations graphically.
Solution:
To solve the given system of linear equations graphically, we need to plot the graph of each equation on the same coordinate plane. The point where the two lines intersect will be the solution to the system.
For each equation, we find at least two points that lie on the line. It is often convenient to find the points where the line intersects the x-axis (by setting $y=0$) and the y-axis (by setting $x=0$), or choose other convenient values for $x$ to find corresponding $y$ values.
For Equation (1): $5x - y = 5$
We can rewrite the equation to express $y$ in terms of $x$:
$y = 5x - 5$
Let's find a few points:
| $x$ | $y = 5x - 5$ | Point $(x, y)$ |
| 0 | $5(0) - 5 = -5$ | (0, -5) |
| 1 | $5(1) - 5 = 5 - 5 = 0$ | (1, 0) |
| 2 | $5(2) - 5 = 10 - 5 = 5$ | (2, 5) |
Plot the points (0, -5), (1, 0), and (2, 5) on a graph paper and draw a straight line passing through them. This is the graph of $5x - y = 5$.
For Equation (2): $3x - y = 3$
We can rewrite the equation to express $y$ in terms of $x$:
$y = 3x - 3$
Let's find a few points:
| $x$ | $y = 3x - 3$ | Point $(x, y)$ |
| 0 | $3(0) - 3 = -3$ | (0, -3) |
| 1 | $3(1) - 3 = 3 - 3 = 0$ | (1, 0) |
| 2 | $3(2) - 3 = 6 - 3 = 3$ | (2, 3) |
Plot the points (0, -3), (1, 0), and (2, 3) on the same graph paper and draw a straight line passing through them. This is the graph of $3x - y = 3$.
Observe the graph where the two lines intersect. From the tables, we can see that the point (1, 0) lies on both lines. Therefore, the lines intersect at the point (1, 0).
The coordinates of the point of intersection give the solution to the system of equations.
$x = 1$
$y = 0$
To verify, substitute these values into the original equations:
For Equation (1): $5(1) - 0 = 5 - 0 = 5$. The equation $5 = 5$ is true.
For Equation (2): $3(1) - 0 = 3 - 0 = 3$. The equation $3 = 3$ is true.
Since the point (1, 0) satisfies both equations, it is the correct solution.
Conclusion:
Graphically, the two lines intersect at the point (1, 0). Therefore, the solution to the given system of equations is $x = 1$ and $y = 0$.
Question 18. If the sum of the first n terms of an AP is 4n – n2, what is the 10th term and the nth term?
OR
How many terms of the AP : 9, 17, 25, ... must be taken to give a sum 636?
Answer:
Given:
The sum of the first $n$ terms of an AP is given by $S_n = 4n - n^2$.
To Find:
The 10th term ($a_{10}$) and the $n$-th term ($a_n$) of the AP.
Solution:
The sum of the first $n$ terms of an AP is given by $S_n$.
The first term of the AP, $a_1$, is equal to the sum of the first term, $S_1$.
$a_1 = S_1$
Substitute $n=1$ into the formula for $S_n$:
$S_1 = 4(1) - (1)^2 = 4 - 1 = 3$
$a_1 = 3$
The sum of the first two terms, $S_2$, is $a_1 + a_2$.
$S_2 = a_1 + a_2$
Substitute $n=2$ into the formula for $S_n$:
$S_2 = 4(2) - (2)^2 = 8 - 4 = 4$
Now, use the relationship $S_2 = a_1 + a_2$ to find $a_2$:
$4 = 3 + a_2$
$a_2 = 4 - 3 = 1$
The first two terms of the AP are $a_1 = 3$ and $a_2 = 1$.
The common difference $d$ of the AP is the difference between consecutive terms:
$d = a_2 - a_1 = 1 - 3 = -2$
Now we can find the $n$-th term of the AP using the formula $a_n = a_1 + (n-1)d$:
$a_n = 3 + (n - 1)(-2)$
$a_n = 3 - 2n + 2$
$a_n = 5 - 2n$
To find the 10th term, we substitute $n=10$ into the formula for $a_n$:
$a_{10} = 5 - 2(10)$
$a_{10} = 5 - 20$
$a_{10} = -15$
Alternate Method (using the relationship between $S_n$ and $a_n$):
The $n$-th term of an AP can also be found using the formula $a_n = S_n - S_{n-1}$, for $n > 1$.
We are given $S_n = 4n - n^2$.
Replace $n$ with $(n-1)$ to find $S_{n-1}$:
$S_{n-1} = 4(n-1) - (n-1)^2$
$= 4n - 4 - (n^2 - 2n + 1)$
$= 4n - 4 - n^2 + 2n - 1$
$S_{n-1} = -n^2 + 6n - 5$
Now, find $a_n = S_n - S_{n-1}$:
$a_n = (4n - n^2) - (-n^2 + 6n - 5)$
$= 4n - n^2 + n^2 - 6n + 5$
$a_n = -2n + 5$
This formula is valid for $n > 1$. For $n=1$, $a_1 = S_1 = 4(1) - 1^2 = 3$. Using the formula $a_n = -2n + 5$ for $n=1$, we get $a_1 = -2(1) + 5 = -2 + 5 = 3$. So the formula $a_n = 5 - 2n$ is valid for all natural numbers $n \geq 1$.
To find the 10th term, substitute $n=10$ into the formula for $a_n$:
$a_{10} = 5 - 2(10) = 5 - 20 = -15$
Conclusion:
The 10th term of the AP is -15.
The $n$-th term of the AP is $a_n = 5 - 2n$.
Question 19. If (1, 2), (4, y), (x, 6) and (3, 5) are the vertices of a parallelogram taken in order, find the values of x and y.
Answer:
Given:
The vertices of a parallelogram taken in order are A(1, 2), B(4, y), C(x, 6), and D(3, 5).
To Find:
The values of $x$ and $y$.
Solution:
In a parallelogram, the diagonals bisect each other. This means that the midpoint of the diagonal AC is the same as the midpoint of the diagonal BD.
Let the vertices be A(1, 2), B(4, y), C(x, 6), and D(3, 5).
We will use the midpoint formula. The midpoint of a line segment with endpoints $(x_1, y_1)$ and $(x_2, y_2)$ is given by $\left(\frac{x_1 + x_2}{2}, \frac{y_1 + y_2}{2}\right)$.
Calculate the midpoint of the diagonal AC:
Midpoint of AC = $\left(\frac{1 + x}{2}, \frac{2 + 6}{2}\right) = \left(\frac{1 + x}{2}, \frac{8}{2}\right) = \left(\frac{1 + x}{2}, 4\right)$
Calculate the midpoint of the diagonal BD:
Midpoint of BD = $\left(\frac{4 + 3}{2}, \frac{y + 5}{2}\right) = \left(\frac{7}{2}, \frac{y + 5}{2}\right)$
Since the midpoints of the diagonals are the same, we can equate the corresponding coordinates:
$\frac{1 + x}{2} = \frac{7}{2}$
... (Equating x-coordinates)
$\frac{8}{2} = \frac{y + 5}{2}$
... (Equating y-coordinates)
Solve the equation for $x$:
$\frac{1 + x}{2} = \frac{7}{2}$
Multiply both sides by 2:
$1 + x = 7$
Subtract 1 from both sides:
$x = 7 - 1$
$x = 6$
Solve the equation for $y$:
$\frac{8}{2} = \frac{y + 5}{2}$
Simplify the left side and multiply both sides by 2:
$4 = \frac{y + 5}{2}$
$4 \times 2 = y + 5$
$8 = y + 5$
Subtract 5 from both sides:
$y = 8 - 5$
$y = 3$
So, the values of $x$ and $y$ are 6 and 3, respectively.
Conclusion:
The values of $x$ and $y$ are $x = 6$ and $y = 3$.
Question 20. The sides AB, BC and median AD of a ∆ABC are respectively propotional to the sides PQ, QR and the median PM of ∆PQR. Show that ∆ABC ~ ∆PQR.
Answer:
Given:
In $\triangle$ABC, AD is the median to side BC. In $\triangle$PQR, PM is the median to side QR.
The sides AB, BC, and median AD of $\triangle$ABC are respectively proportional to the sides PQ, QR, and the median PM of $\triangle$PQR.
$\frac{AB}{PQ} = \frac{BC}{QR} = \frac{AD}{PM}$
... (1)
To Prove:
$\triangle$ABC ~ $\triangle$PQR (Triangle ABC is similar to Triangle PQR).
Proof:
We are given that AD and PM are medians. A median divides the opposite side into two equal halves.
In $\triangle$ABC, AD is the median to BC, so BD = DC = $\frac{1}{2}$ BC.
$BD = \frac{1}{2} BC$
In $\triangle$PQR, PM is the median to QR, so QM = MR = $\frac{1}{2}$ QR.
$QM = \frac{1}{2} QR$
From the given proportionality (1), we have:
$\frac{AB}{PQ} = \frac{BC}{QR} = \frac{AD}{PM}$
We can rewrite the ratio of BC to QR in terms of their halves:
$\frac{BC}{QR} = \frac{2 \times BD}{2 \times QM} = \frac{BD}{QM}$
So, the given proportionality can be written as:
$\frac{AB}{PQ} = \frac{BD}{QM} = \frac{AD}{PM}$
... (2)
Consider $\triangle$ABD and $\triangle$PQM.
From equation (2), the ratios of their corresponding sides are equal:
$\frac{AB}{PQ} = \frac{BD}{QM} = \frac{AD}{PM}$
According to the SSS similarity criterion, if the corresponding sides of two triangles are proportional, then the triangles are similar.
Therefore, by SSS similarity criterion:
$\triangle ABD \sim \triangle PQM$
Since $\triangle$ABD is similar to $\triangle$PQM, their corresponding angles are equal.
In particular, the angles opposite to the proportional sides are equal. The angle opposite to AD in $\triangle$ABD is $\angle ABD$ (which is $\angle ABC$). The angle opposite to PM in $\triangle$PQM is $\angle PQM$ (which is $\angle PQR$).
$\angle ABD = \angle PQM$
Since D lies on BC and M lies on QR, we can write:
$\angle ABC = \angle PQR$
... (3)
Now consider the main triangles $\triangle$ABC and $\triangle$PQR.
From the given information (1), we have the proportionality of two sides:
$\frac{AB}{PQ} = \frac{BC}{QR}$
... (4)
And from equation (3), we have the equality of the included angle between these two sides:
$\angle ABC = \angle PQR$
(Included angle)
According to the SAS similarity criterion, if two sides of one triangle are proportional to two sides of another triangle and the included angles are equal, then the two triangles are similar.
Therefore, by SAS similarity criterion:
$\triangle ABC \sim \triangle PQR$
This completes the proof.
Conclusion:
Based on the proportionality of sides AB, BC, and median AD of $\triangle$ABC to the corresponding sides PQ, QR, and median PM of $\triangle$PQR, we have shown that $\triangle$ABC is similar to $\triangle$PQR using the SSS similarity of $\triangle$ABD and $\triangle$PQM to establish the equality of included angles, and then applying the SAS similarity criterion to $\triangle$ABC and $\triangle$PQR.
Question 21. A triangle ABC is drawn to circumscribe a circle of radius 4 cm such that the segments BD and DC into which BC is divided by the point of contact D are of lengths 8 cm and 7 cm, respectively. Find the sides AB and AC.
Answer:
Given:
Triangle ABC circumscribes a circle with radius $r = 4$ cm.
Point of contact on BC is D. BD = 8 cm, DC = 7 cm.
To Find:
Lengths of sides AB and AC.
Solution:
Let the circle touch AB at F and AC at E.
By the property of tangents from an external point:
BF = BD = 8 cm
CE = CD = 7 cm
Let AF = AE = $x$ cm.
The sides of the triangle are:
AB = AF + FB = $(x + 8)$ cm
AC = AE + EC = $(x + 7)$ cm
BC = BD + DC = $8 + 7 = 15$ cm
The semi-perimeter $s$ of $\triangle$ABC is:
$s = \frac{(x+8) + (x+7) + 15}{2} = \frac{2x + 30}{2} = (x + 15)$ cm
The area of $\triangle$ABC can be calculated using two methods:
1. Using inradius: Area = $rs$
Area = $4(x + 15)$
... (1)
2. Using Heron's formula: Area = $\sqrt{s(s-a)(s-b)(s-c)}$
Here, $s-a = (x+15)-15 = x$, $s-b = (x+15)-(x+7)=8$, $s-c = (x+15)-(x+8)=7$.
Area = $\sqrt{(x+15)(x)(8)(7)} = \sqrt{56x(x+15)}$
... (2)
Equating (1) and (2):
$4(x + 15) = \sqrt{56x(x + 15)}$
Square both sides:
$16(x + 15)^2 = 56x(x + 15)$
Since $x > 0$, $x+15 \neq 0$. Divide both sides by $8(x+15)$:
$\frac{\cancel{16}^2 \cancel{(x + 15)}}{\cancel{8}} = \frac{\cancel{56}^7 x}{\cancel{8}}$
$2(x + 15) = 7x$
$2x + 30 = 7x$
$30 = 5x$
$x = 6$ cm
Substitute $x=6$ into the expressions for AB and AC:
AB = $6 + 8 = 14$ cm
AC = $6 + 7 = 13$ cm
Conclusion:
The lengths of sides AB and AC are 14 cm and 13 cm, respectively.
Question 22. Construct an isosceles triangle whose base is 6 cm and altitude 5 cm and then another triangle whose sides are $\frac{7}{5}$ of the corresponding sides of the isosceles triangle.
Answer:
Given:
An isosceles triangle with base 6 cm and altitude 5 cm.
A required triangle whose sides are $\frac{7}{5}$ times the corresponding sides of the isosceles triangle.
To Construct:
1. An isosceles triangle with base 6 cm and altitude 5 cm.
2. A similar triangle whose sides are $\frac{7}{5}$ times the sides of the first triangle.
Construction Steps:
1. Draw a line segment BC = 6 cm.
2. Draw the perpendicular bisector of BC. Let D be the midpoint of BC.
3. Along the perpendicular bisector from D, mark a point A such that AD = 5 cm. Since AD is the altitude to the base of an isosceles triangle, A must lie on the perpendicular bisector for AB = AC.
4. Join AB and AC. $\triangle$ABC is the required isosceles triangle with base BC = 6 cm and altitude AD = 5 cm.
5. Draw a ray BX from B, making an acute angle ($\angle CBX$) with BC. The ray BX should be on the opposite side of vertex A relative to BC.
6. Locate 7 points (the greater of 7 and 5) $B_1, B_2, B_3, B_4, B_5, B_6, B_7$ on ray BX such that $BB_1 = B_1B_2 = B_2B_3 = B_3B_4 = B_4B_5 = B_5B_6 = B_6B_7$.
7. Join $B_5$ (corresponding to the denominator 5) to C.
8. Draw a line through $B_7$ (corresponding to the numerator 7) parallel to $B_5C$, intersecting the extended line segment BC at point C'.
9. Draw a line through C' parallel to AC, intersecting the extended line segment BA at point A'.
10. $\triangle$A'BC' is the required triangle whose sides are $\frac{7}{5}$ of the corresponding sides of $\triangle$ABC.
Justification:
By construction, $B_7C' \parallel B_5C$. In $\triangle BB_7C$, by the Basic Proportionality Theorem (or by AA similarity of $\triangle BB_5C$ and $\triangle BB_7C'$ since $\angle B$ is common and $\angle BB_5C = \angle BB_7C'$ as corresponding angles), we have $\frac{BC}{BC'} = \frac{BB_5}{BB_7}$.
By construction, $\frac{BB_5}{BB_7} = \frac{5}{7}$.
$\frac{BC}{BC'} = \frac{5}{7}$
$BC' = \frac{7}{5} BC$
Also, by construction, A'C' $\parallel$ AC. In $\triangle$BAC and $\triangle$BA'C', $\angle BAC = \angle BA'C'$ (corresponding angles) and $\angle B$ is common. Therefore, $\triangle BAC \sim \triangle BA'C'$ by AA similarity criterion.
For similar triangles, the ratio of corresponding sides is equal:
$\frac{BA'}{BA} = \frac{BC'}{BC} = \frac{A'C'}{AC}$
Since $\frac{BC'}{BC} = \frac{7}{5}$, we have:
$\frac{BA'}{BA} = \frac{7}{5}$
$\frac{A'C'}{AC} = \frac{7}{5}$
Thus, the sides of $\triangle$A'BC' are $\frac{7}{5}$ times the corresponding sides of $\triangle$ABC.
Question 23. Prove that $\frac{\cos\;\theta \;-\; \sin\;\theta\;+\;1}{\sin\;\theta\;+\;\cos\;\theta\;-\;1}=\frac{1}{cosec\;\theta\;-\;\cot\;\theta}$
OR
Evaluate:
$\left( \frac{3cos \;43^\circ}{sin \;47^\circ} \right)^2 - \frac{cos \;37^\circ\; cosec\;53^\circ}{tan \;5^\circ \;tan \;25^\circ \;tan \;45^\circ \;tan \;65^\circ \;tan \;85^\circ}$
Answer:
Given:
The identity to prove: $\frac{\cos\;\theta \;-\; \sin\;\theta\;+\;1}{\sin\;\theta\;+\;\cos\;\theta\;-\;1}=\frac{1}{cosec\;\theta\;-\;\cot\;\theta}$.
To Prove:
$\frac{\cos\;\theta \;-\; \sin\;\theta\;+\;1}{\sin\;\theta\;+\;\cos\;\theta\;-\;1}=\frac{1}{cosec\;\theta\;-\;\cot\;\theta}$.
Proof:
Let's start with the Left Hand Side (LHS) of the identity.
LHS = $\frac{\cos\;\theta \;-\; \sin\;\theta\;+\;1}{\sin\;\theta\;+\;\cos\;\theta\;-\;1}$
To introduce $\text{cosec}\theta$ and $\cot\theta$, divide the numerator and the denominator by $\sin\theta$. This is valid assuming $\sin\theta \neq 0$ (which is required for $\text{cosec}\theta$ and $\cot\theta$ to be defined).
LHS = $\frac{\frac{\cos\theta}{\sin\theta} - \frac{\sin\theta}{\sin\theta} + \frac{1}{\sin\theta}}{\frac{\sin\theta}{\sin\theta} + \frac{\cos\theta}{\sin\theta} - \frac{1}{\sin\theta}}$
Using the trigonometric identities $\cot\theta = \frac{\cos\theta}{\sin\theta}$ and $\text{cosec}\theta = \frac{1}{\sin\theta}$:
LHS = $\frac{\cot\theta - 1 + \text{cosec}\theta}{1 + \cot\theta - \text{cosec}\theta}$
Rearrange the terms in the numerator to group $\text{cosec}\theta + \cot\theta$:
LHS = $\frac{(\text{cosec}\theta + \cot\theta) - 1}{1 + \cot\theta - \text{cosec}\theta}$
Using the fundamental identity $\text{cosec}^2\theta - \cot^2\theta = 1$, we can replace the '1' in the numerator with $(\text{cosec}^2\theta - \cot^2\theta)$.
LHS = $\frac{(\text{cosec}\theta + \cot\theta) - (\text{cosec}^2\theta - \cot^2\theta)}{1 + \cot\theta - \text{cosec}\theta}$
Factor the term $(\text{cosec}^2\theta - \cot^2\theta)$ using the difference of squares formula, $a^2 - b^2 = (a-b)(a+b)$.
LHS = $\frac{(\text{cosec}\theta + \cot\theta) - (\text{cosec}\theta - \cot\theta)(\text{cosec}\theta + \cot\theta)}{1 + \cot\theta - \text{cosec}\theta}$
Factor out the common term $(\text{cosec}\theta + \cot\theta)$ from the two terms in the numerator:
LHS = $\frac{(\text{cosec}\theta + \cot\theta) [1 - (\text{cosec}\theta - \cot\theta)]}{1 + \cot\theta - \text{cosec}\theta}$
LHS = $\frac{(\text{cosec}\theta + \cot\theta) [1 - \text{cosec}\theta + \cot\theta]}{1 + \cot\theta - \text{cosec}\theta}$
Notice that the term in the square brackets $[1 - \text{cosec}\theta + \cot\theta]$ is exactly the same as the denominator $1 + \cot\theta - \text{cosec}\theta$. Assuming the denominator is not zero, we can cancel the common term.
LHS = $\text{cosec}\theta + \cot\theta$
... (1)
Now let's simplify the Right Hand Side (RHS) of the identity.
RHS = $\frac{1}{\text{cosec}\;\theta\;-\;\cot\;\theta}$
To simplify this expression and make it resemble the form we got for the LHS, we can multiply the numerator and denominator by the conjugate of the denominator, which is $(\text{cosec}\theta + \cot\theta)$.
RHS = $\frac{1}{(\text{cosec}\theta - \cot\theta)} \times \frac{(\text{cosec}\theta + \cot\theta)}{(\text{cosec}\theta + \cot\theta)}$
RHS = $\frac{\text{cosec}\theta + \cot\theta}{(\text{cosec}\theta - \cot\theta)(\text{cosec}\theta + \cot\theta)}$
Apply the difference of squares formula $(a-b)(a+b) = a^2 - b^2$ to the denominator:
RHS = $\frac{\text{cosec}\theta + \cot\theta}{\text{cosec}^2\theta - \cot^2\theta}$
Using the identity $\text{cosec}^2\theta - \cot^2\theta = 1$ in the denominator:
RHS = $\frac{\text{cosec}\theta + \cot\theta}{1}$
RHS = $\text{cosec}\theta + \cot\theta$
... (2)
From equation (1) and equation (2), we have shown that LHS = $\text{cosec}\theta + \cot\theta$ and RHS = $\text{cosec}\theta + \cot\theta$.
Therefore, LHS = RHS.
Conclusion:
The identity $\frac{\cos\;\theta \;-\; \sin\;\theta\;+\;1}{\sin\;\theta\;+\;\cos\;\theta\;-\;1}=\frac{1}{cosec\;\theta\;-\;\cot\;\theta}$ is proven.
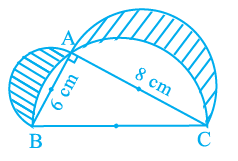
Question 24. In the figure, ABC is a triangle right angled at A. Semicircles are drawn on AB, AC and BC as diameters. Find the area of the shaded region.
Answer:
Given:
A triangle ABC is right-angled at A.
Semicircles are drawn on the sides AB, AC, and BC as diameters.
To Find:
The area of the shaded region.
Solution:
Let the lengths of the sides of the right-angled triangle ABC be:
AB = $c$
AC = $b$
BC = $a$
Since $\triangle$ABC is right-angled at A, according to the Pythagorean theorem, we have:
$a^2 = b^2 + c^2$
... (Pythagorean theorem)
The area of a semicircle with diameter $d$ (and radius $r = d/2$) is given by $\frac{1}{2} \pi r^2 = \frac{1}{2} \pi (\frac{d}{2})^2 = \frac{\pi d^2}{8}$.
Area of the semicircle on AB (diameter $c$):
Area$_{AB}$ = $\frac{\pi c^2}{8}$
Area of the semicircle on AC (diameter $b$):
Area$_{AC}$ = $\frac{\pi b^2}{8}$
Area of the semicircle on BC (diameter $a$):
Area$_{BC}$ = $\frac{\pi a^2}{8}$
The area of the right-angled triangle ABC is:
Area$_{\triangle ABC}$ = $\frac{1}{2} \times \text{base} \times \text{height} = \frac{1}{2} \times AC \times AB = \frac{1}{2} bc$
The shaded region consists of the areas of the two semicircles on AB and AC, plus the area of the triangle ABC, minus the area of the semicircle on BC (which covers the triangle and parts of the other two semicircles).
Area of Shaded Region = Area$_{AB}$ + Area$_{AC}$ + Area$_{\triangle ABC}$ - Area$_{BC}$
Substitute the expressions for the areas:
Area of Shaded Region = $\frac{\pi c^2}{8} + \frac{\pi b^2}{8} + \frac{1}{2} bc - \frac{\pi a^2}{8}$
Group the terms with $\pi$:
Area of Shaded Region = $\frac{\pi}{8} (c^2 + b^2 - a^2) + \frac{1}{2} bc$
From the Pythagorean theorem, we know that $c^2 + b^2 = a^2$. Therefore, $c^2 + b^2 - a^2 = 0$.
Substitute this into the expression for the shaded area:
Area of Shaded Region = $\frac{\pi}{8} (0) + \frac{1}{2} bc$
Area of Shaded Region = $\frac{1}{2} bc$
We see that the area of the shaded region is equal to the area of the triangle ABC.
Area of Shaded Region = Area$_{\triangle ABC}$
Since the side lengths are not given numerically, the area of the shaded region is simply equal to the area of the triangle ABC.
Conclusion:
The area of the shaded region is equal to the area of the triangle ABC, which is $\frac{1}{2} \times AB \times AC$.
Question 25. A bag contains white, black and red balls only. A ball is drawn at random from the bag. The probability of getting a white ball is $\frac{3}{10}$ and that of a black ball is $\frac{2}{5}$ . Find the probability of getting a red ball. If the bag contains 20 black balls, then find the total number of balls in the bag.
Answer:
Given:
A bag contains white, black, and red balls only.
Probability of getting a white ball, $P(\text{White}) = \frac{3}{10}$.
Probability of getting a black ball, $P(\text{Black}) = \frac{2}{5}$.
Number of black balls in the bag = 20.
To Find:
1. The probability of getting a red ball, $P(\text{Red})$.
2. The total number of balls in the bag.
Solution:
Since the bag contains only white, black, and red balls, these are the only possible outcomes when a ball is drawn at random. The sum of the probabilities of all elementary events in an experiment is 1.
$P(\text{White}) + P(\text{Black}) + P(\text{Red}) = 1$
Substitute the given probabilities into the equation:
$\frac{3}{10} + \frac{2}{5} + P(\text{Red}) = 1$
To add the fractions, find a common denominator, which is 10:
$\frac{3}{10} + \frac{2 \times 2}{5 \times 2} + P(\text{Red}) = 1$
$\frac{3}{10} + \frac{4}{10} + P(\text{Red}) = 1$
$\frac{3 + 4}{10} + P(\text{Red}) = 1$
$\frac{7}{10} + P(\text{Red}) = 1$
Subtract $\frac{7}{10}$ from both sides to find $P(\text{Red})$:
$P(\text{Red}) = 1 - \frac{7}{10} = \frac{10}{10} - \frac{7}{10} = \frac{3}{10}$
So, the probability of getting a red ball is $\frac{3}{10}$.
Now, we need to find the total number of balls in the bag. Let the total number of balls be $N$.
The probability of getting a black ball is given by the number of black balls divided by the total number of balls.
$P(\text{Black}) = \frac{\text{Number of black balls}}{\text{Total number of balls}}$
We are given $P(\text{Black}) = \frac{2}{5}$ and the number of black balls is 20. Let the total number of balls be $N$.
$\frac{2}{5} = \frac{20}{N}$
To solve for $N$, we can cross-multiply:
$2 \times N = 5 \times 20$
$2N = 100$
Divide both sides by 2:
$N = \frac{100}{2} = 50$
The total number of balls in the bag is 50.
Conclusion:
The probability of getting a red ball is $\frac{3}{10}$.
The total number of balls in the bag is 50.
Section D
Question 26. If the price of a book is reduced by Rs 5, a person can buy 5 more books for Rs 300. Find the original list price of the book.
OR
The sum of the ages of two friends is 20 years. Four years ago, the product of their ages in years was 48. Is this situation possible? If so, determine their present ages.
Answer:
Given:
Total amount available to buy books = $\textsf{₹} 300$.
Price reduction per book = $\textsf{₹} 5$.
Number of extra books that can be bought = 5.
To Find:
The original list price of the book.
Solution:
Let the original list price of the book be $\textsf{₹} x$.
The number of books that could be bought for $\textsf{₹} 300$ at the original price is $\frac{300}{x}$.
Number of books at original price = $\frac{300}{x}$
When the price is reduced by $\textsf{₹} 5$, the new price of the book is $\textsf{₹} (x - 5)$.
The number of books that can be bought for $\textsf{₹} 300$ at the reduced price is $\frac{300}{x - 5}$.
Number of books at reduced price = $\frac{300}{x - 5}$
According to the problem, the person can buy 5 more books at the reduced price.
Number of books at reduced price = (Number of books at original price) + 5
Substitute the expressions for the number of books:
$\frac{300}{x - 5} = \frac{300}{x} + 5$
We need to solve this equation for $x$. First, move the term $\frac{300}{x}$ to the left side:
$\frac{300}{x - 5} - \frac{300}{x} = 5$
Find a common denominator on the left side, which is $x(x - 5)$:
$\frac{300x - 300(x - 5)}{x(x - 5)} = 5$
Expand the numerator:
$\frac{300x - 300x + 1500}{x^2 - 5x} = 5$
Simplify the numerator:
$\frac{1500}{x^2 - 5x} = 5$
Multiply both sides by $(x^2 - 5x)$ (assuming $x \neq 0$ and $x \neq 5$):
$1500 = 5(x^2 - 5x)$
Divide both sides by 5:
$\frac{1500}{5} = x^2 - 5x$
$300 = x^2 - 5x$
Rearrange the equation into a standard quadratic form $ax^2 + bx + c = 0$:
$x^2 - 5x - 300 = 0$
Now, we can solve this quadratic equation by factorization. We need two numbers that multiply to -300 and add up to -5. These numbers are -20 and 15.
$x^2 - 20x + 15x - 300 = 0$
Group the terms and factor:
$(x^2 - 20x) + (15x - 300) = 0$
$x(x - 20) + 15(x - 20) = 0$
Factor out the common term $(x - 20)$:
$(x - 20)(x + 15) = 0$
Set each factor equal to zero to find the possible values of $x$:
Case 1:
$x - 20 = 0 \implies x = 20$
Case 2:
$x + 15 = 0 \implies x = -15$
Since $x$ represents the original price of a book, it must be a positive value. Therefore, $x = -15$ is not a valid solution in this context.
The original list price of the book is $\textsf{₹} 20$.
Verification:
Original price = $\textsf{₹} 20$. Number of books = $\frac{300}{20} = 15$.
Reduced price = $\textsf{₹} 20 - \textsf{₹} 5 = \textsf{₹} 15$.
Number of books at reduced price = $\frac{300}{15} = 20$.
Number of extra books = $20 - 15 = 5$. This matches the given information.
Conclusion:
The original list price of the book is $\textsf{₹} 20$.
Question 27. Prove that the lengths of the tangents drawn from an external point to a circle are equal.
Using the above theorem, prove that:
If quadrilateral ABCD is circumscribing a circle, then AB + CD = AD + BC.
OR
Prove that the ratio of the areas of two similar triangles is equal to the ratio of the squares of the corresponding sides.
Using the above theorem, do the following :
ABC is an iscosceles triangle right angled at B. Two equilateral triangles ACD and ABE are constructed on the sides AC and AB, respectively. Find the ratio of the areas of ∆ABE and ∆ACD.
Answer:
Part 1: Prove that the lengths of the tangents drawn from an external point to a circle are equal.
Given:
A circle with centre O.
An external point P.
Two tangents PA and PB drawn from P to the circle, touching the circle at points A and B respectively.
To Prove:
PA = PB (The lengths of the tangents from P are equal).
Construction:
Join OA, OB, and OP.
Proof:
We know that the radius through the point of contact is perpendicular to the tangent at that point.
$OA \perp PA$
(Radius is perpendicular to tangent at point of contact)
$OB \perp PB$
(Radius is perpendicular to tangent at point of contact)
This means that $\angle OAP$ and $\angle OBP$ are right angles.
$\angle OAP = 90^\circ$
$\angle OBP = 90^\circ$
Now, consider the two right-angled triangles, $\triangle OAP$ and $\triangle OBP$.
In $\triangle OAP$ and $\triangle OBP$:
OA = OB
(Radii of the same circle)
OP = OP
(Common hypotenuse)
$\angle OAP = \angle OBP$
($90^\circ$ each)
Therefore, by the Right Angle - Hypotenuse - Side (RHS) congruence criterion:
$\triangle OAP \cong \triangle OBP$
Since the triangles are congruent, their corresponding parts are equal (CPCT).
PA = PB
(Corresponding sides of congruent triangles)
Thus, the lengths of the tangents drawn from an external point to a circle are equal.
Part 2: Prove that if quadrilateral ABCD is circumscribing a circle, then AB + CD = AD + BC.
Given:
A quadrilateral ABCD circumscribes a circle.
To Prove:
AB + CD = AD + BC.
Proof:
Let the circle touch the sides AB, BC, CD, and DA at points P, Q, R, and S respectively.
Using the theorem proven in Part 1 (lengths of tangents from an external point to a circle are equal), we have the following equalities:
From external point A, tangents are AP and AS:
AP = AS
... (1)
From external point B, tangents are BP and BQ:
BP = BQ
... (2)
From external point C, tangents are CR and CQ:
CR = CQ
... (3)
From external point D, tangents are DR and DS:
DR = DS
... (4)
Add the equations (1), (2), (3), and (4):
$(AP + BP + CR + DR) = (AS + BQ + CQ + DS)$
Rearrange the terms on both sides:
$(AP + BP) + (CR + DR) = (AS + DS) + (BQ + CQ)$
Recognize that:
AP + BP = AB
(P lies on AB)
CR + DR = CD
(R lies on CD)
AS + DS = AD
(S lies on AD)
BQ + CQ = BC
(Q lies on BC)
Substitute these into the rearranged equation:
AB + CD = AD + BC
Thus, for a quadrilateral circumscribing a circle, the sum of opposite sides are equal.
Conclusion:
The property AB + CD = AD + BC for a circumscribing quadrilateral is proven using the theorem that tangents from an external point to a circle are equal in length.
Question 28. The angles of depression of the top and bottom of a building 50 metres high as observed from the top of a tower are 30° and 60°, respectively. Find the height of the tower and also the horizontal distances between the building and the tower.
Answer:
Given:
Height of the building = 50 metres.
Angle of depression of the top of the building from the top of the tower = $30^\circ$.
Angle of depression of the bottom of the building from the top of the tower = $60^\circ$.
To Find:
1. The height of the tower.
2. The horizontal distance between the building and the tower.
Solution:
Let the height of the tower be TG = $H$ metres and the height of the building be BF = 50 metres.
Let the horizontal distance between the building and the tower be GF = $D$ metres.
Let T be the top of the tower and G be the bottom of the tower. Let B be the top of the building and F be the bottom of the building.
Draw a horizontal line TE from the top of the tower T, parallel to the ground GF.
The angle of depression to the top of the building B is $\angle ETB = 30^\circ$.
The angle of depression to the bottom of the building F is $\angle ETF = 60^\circ$.
Since TE is parallel to GF, and TF is a transversal, the alternate interior angle is $\angle TFG = \angle ETF = 60^\circ$.
Since TE is parallel to the horizontal line BF extended, and TB is a transversal, draw a horizontal line BC from B to meet TG at C. Then $\angle TBC = \angle ETB = 30^\circ$.
In the figure, BCFG forms a rectangle, so BC = GF = $D$ and CG = BF = 50 metres.
The height of the tower is $H = TG = TC + CG = TC + 50$ metres.
Consider the right-angled triangle $\triangle TFG$.
$\tan (\angle TFG) = \frac{TG}{FG}$
$\tan 60^\circ = \frac{H}{D}$
$\sqrt{3} = \frac{H}{D}$
$H = D\sqrt{3}$
... (1)
Consider the right-angled triangle $\triangle TBC$. The height TC = H - 50 and the base BC = D.
$\tan (\angle TBC) = \frac{TC}{BC}$
$\tan 30^\circ = \frac{H - 50}{D}$
$\frac{1}{\sqrt{3}} = \frac{H - 50}{D}$
$D = \sqrt{3}(H - 50)$
... (2)
Now we have a system of two linear equations in terms of H and D. Substitute the value of D from equation (1) into equation (2):
$\frac{H}{\sqrt{3}} = \sqrt{3}(H - 50)$
Multiply both sides by $\sqrt{3}$:
$H = 3(H - 50)$
$H = 3H - 150$
Rearrange the equation to solve for H:
$150 = 3H - H$
$150 = 2H$
$H = \frac{150}{2} = 75$ metres
Now find the horizontal distance D using equation (1):
$D = \frac{H}{\sqrt{3}} = \frac{75}{\sqrt{3}}$
To rationalize the denominator, multiply the numerator and denominator by $\sqrt{3}$:
$D = \frac{75}{\sqrt{3}} \times \frac{\sqrt{3}}{\sqrt{3}} = \frac{75\sqrt{3}}{3}$
$D = 25\sqrt{3}$ metres
Conclusion:
The height of the tower is 75 metres.
The horizontal distance between the building and the tower is $25\sqrt{3}$ metres.
Question 29. A well of diameter 3 m and 14 m deep is dug. The earth, taken out of it, has been evenly spread all around it in the shape of a circular ring of width 4 m to form an embankment . Find the height of the embankment.
Answer:
Given:
Diameter of the well = 3 m. Radius of the well, $r_w = \frac{3}{2} = 1.5$ m.
Depth of the well, $h_w = 14$ m.
Width of the circular ring (embankment) = 4 m.
To Find:
The height of the embankment.
Solution:
The earth dug out from the well is used to form the embankment. This means the volume of earth dug out from the well is equal to the volume of the embankment.
The well is in the shape of a cylinder. The volume of the well (and the earth dug out) is given by the formula for the volume of a cylinder, $V = \pi r^2 h$.
Volume of earth dug out = Volume of cylinder (well)
Volume of earth = $\pi r_w^2 h_w$
Substitute the values of $r_w$ and $h_w$:
Volume of earth = $\pi (1.5)^2 (14)$
Volume of earth = $\pi (2.25)(14)$
Volume of earth = $31.5\pi \text{ m}^3$
... (1)
The embankment is in the shape of a circular ring around the well. It can be considered as a hollow cylinder. The inner radius of the embankment is the radius of the well, $r_1 = r_w = 1.5$ m.
The outer radius of the embankment is the inner radius plus the width of the ring.
Outer radius of embankment, $r_2 = r_w + \text{width} = 1.5 + 4 = 5.5$ m
Let the height of the embankment be $h_e$.
The volume of the embankment is the volume of the outer cylinder minus the volume of the inner cylinder (the space of the well). This is also the area of the ring base multiplied by the height.
Area of the circular ring base = Area of outer circle - Area of inner circle
Area of ring base = $\pi r_2^2 - \pi r_1^2 = \pi (r_2^2 - r_1^2)$
Substitute the values of $r_1$ and $r_2$:
Area of ring base = $\pi ((5.5)^2 - (1.5)^2)$
$= \pi (30.25 - 2.25)$
Area of ring base = $28\pi \text{ m}^2$
The volume of the embankment is the area of the ring base multiplied by the height of the embankment:
Volume of embankment = (Area of ring base) $\times h_e$
Volume of embankment = $28\pi h_e \text{ m}^3$
... (2)
Since the volume of earth dug out equals the volume of the embankment, we equate equation (1) and equation (2):
Volume of earth dug out = Volume of embankment
$31.5\pi = 28\pi h_e$
Divide both sides by $28\pi$ to solve for $h_e$:
$h_e = \frac{31.5\pi}{28\pi}$
$h_e = \frac{31.5}{28}$
To simplify the fraction, multiply the numerator and denominator by 10 to remove the decimal:
$h_e = \frac{315}{280}$
Divide the numerator and denominator by their greatest common divisor, which is 35:
$h_e = \frac{\cancel{315}^9}{\cancel{280}_8} = \frac{9}{8}$
Express the height as a decimal:
$h_e = 1.125$ metres
Conclusion:
The height of the embankment is 1.125 metres.
Question 30. The following table shows the ages of the patients admitted in a hospital during a month:
| Age (in years) | 5 - 15 | 15 - 25 | 25 - 35 | 35 - 45 | 45 - 55 | 55 - 65 |
|---|---|---|---|---|---|---|
| Number of patients | 6 | 11 | 21 | 23 | 14 | 5 |
Find the mode and the mean of the data given above.
Answer:
Given:
Frequency distribution table showing the ages of patients in a hospital.
To Find:
The mode and the mean of the given data.
Solution - Mode:
The mode is the value that appears most frequently in a data set. In a grouped frequency distribution, the mode is given by the formula:
$Mode = l + \frac{f_1 - f_0}{2f_1 - f_0 - f_2} \times h$
... (Mode formula for grouped data)
First, we identify the modal class, which is the class interval with the highest frequency.
From the table, the highest frequency is 23, which corresponds to the class interval 35 - 45.
So, the modal class is 35 - 45.
From the modal class, we have:
Lower limit of the modal class, $l = 35$
Frequency of the modal class, $f_1 = 23$
Frequency of the class preceding the modal class, $f_0 = 21$ (for class 25 - 35)
Frequency of the class succeeding the modal class, $f_2 = 14$ (for class 45 - 55)
The class size, $h = 15 - 5 = 10$. (The class size is uniform across all intervals).
Substitute these values into the mode formula:
$Mode = 35 + \frac{23 - 21}{2(23) - 21 - 14} \times 10$
$= 35 + \frac{2}{46 - 35} \times 10$
$= 35 + \frac{2}{11} \times 10$
$= 35 + \frac{20}{11}$
$= 35 + 1.8181...$
$Mode \approx 36.82$ years
Solution - Mean:
We will use the Step Deviation Method to find the mean. The formula for the mean is:
$Mean (\bar{x}) = a + \frac{\sum f_i u_i}{\sum f_i} \times h$
... (Mean formula - Step Deviation Method)
First, calculate the class mark ($x_i$) for each interval and set up the columns for the calculations.
Let's choose the assumed mean $a = 40$ (the class mark of the modal class).
The class size $h = 10$.
| Age (in years) | Number of patients ($f_i$) | Class Mark ($x_i$) | $d_i = x_i - a = x_i - 40$ | $u_i = d_i / h = d_i / 10$ | $f_i u_i$ |
| 5 - 15 | 6 | 10 | -30 | -3 | -18 |
| 15 - 25 | 11 | 20 | -20 | -2 | -22 |
| 25 - 35 | 21 | 30 | -10 | -1 | -21 |
| 35 - 45 | 23 | 40 | 0 | 0 | 0 |
| 45 - 55 | 14 | 50 | 10 | 1 | 14 |
| 55 - 65 | 5 | 60 | 20 | 2 | 10 |
| Total | $\sum f_i = 80$ | $\sum f_i u_i = -37$ |
Now, substitute the values into the mean formula:
$Mean = 40 + \frac{-37}{80} \times 10$
$= 40 + \frac{-370}{80}$
$= 40 - \frac{37}{8}$
$= 40 - 4.625$
$Mean = 35.375$ years
Conclusion:
The mode of the data is approximately 36.82 years.
The mean of the data is 35.375 years.

